Surfaces of revolution • from [Kü03] pp.52-54
We walk thru the computations carried out on pages 53-54 in [Kü03] to compare the results.
![]()
![]()
![]()
![]()
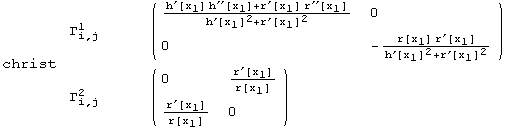
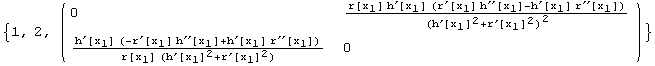
![]()
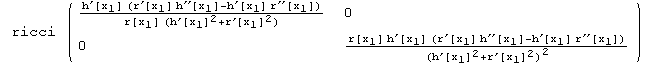
![]()
We make the same assumptions as [Kü03].
![]()
![]()
![]()
![]()
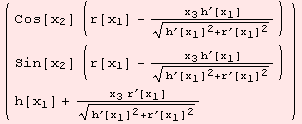
![]()
All figures below are labelled. Without additional assumptions, the geometrical expressions get quite complicated.
![]()
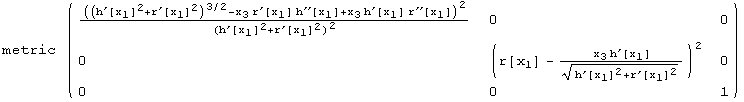
![]()
 |
|
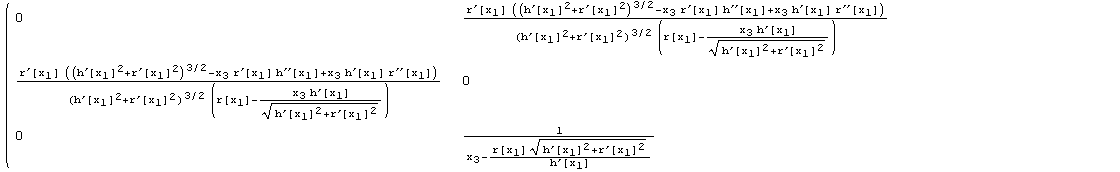 |
|
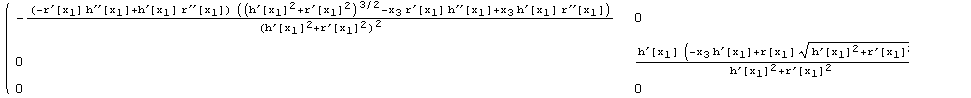 |
![]()
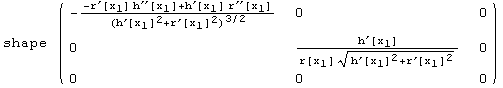
![]()
To simplify the discussion, at this point [Kü03] makes the stronger assuptions that the curve (r,h) is parametrised according to arc length.
![]()
![]()
![]()
![]()
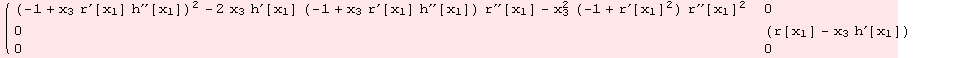
![( {{1, 0, 0}, {0, r[x_1]^2, 0}, {0, 0, 1}} )](../HTMLFiles/index_343.gif)
All expressions are labelled:
![]()
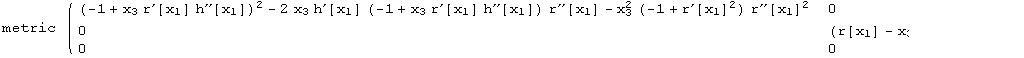
![]()
 |
|
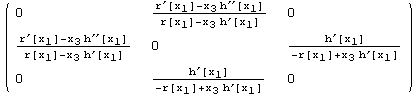 |
|
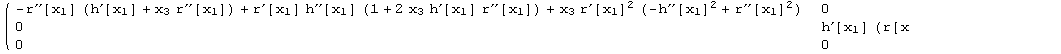 |
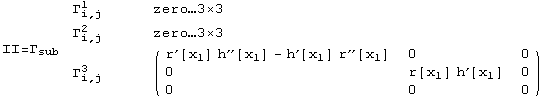
![shape= ( {{r^′[x_1] h^′′[x_1] - h^′[x_1] r^′′[x_1], 0, 0}, {0, h^′[x_1]/r[x_1], 0}, {0, 0, 0}} )](../HTMLFiles/index_354.gif)
![]()
![]()
![]()
![]()
| Created by Mathematica (December 22, 2006) |