Commutator vector field

U = x_2 {Sin[x_1], Cos[x_1]} ;

V = {x_1 x_2, x_1^2 + x_2} ;

ΜCom[U, V]//S

{-Cos[x_1] x_1 (-1 + x_2) x_2 - Sin[x_1] (x_1^2 + x_2 - x_2^2), x_1 (-Cos[x_1] x_1 + Sin[x_1] x_2 (2 + x_2))}

PlotVectorField[#1, {x_1, 0, π}, {x_2, 0, π}, PlotPoints→10, Frame→True, PlotRange→ {{-.1, π + .1}, {-.1, π + .1}}] &/@{U, V, ΜCom[U, V]} ;

[Graphics:../HTMLFiles/index_29.gif]

[Graphics:../HTMLFiles/index_30.gif]

[Graphics:../HTMLFiles/index_31.gif]

pα = ParametricPlot[Evaluate[Χα[U, {1, #1}, {-1, 2}] &/@Range[1, 3, .333]], {, -1, 2}, DisplayFunction→Identity] ;

[Graphics:../HTMLFiles/index_34.gif]

? ΜCom

Global`ΜCom

ΜCom[X_,Y_]:=Μd[Y,1].X-Μd[X,1].Y

The following set of vector fields is closed under the commutator.

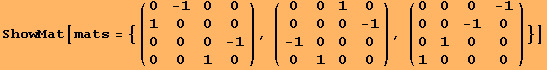
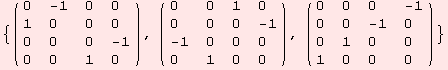
{( {{0, -1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, -1}, {0, 0, 1, 0}} ), ( {{0, 0, 1, 0}, {0, 0, 0, -1}, {-1, 0, 0, 0}, {0, 1, 0, 0}} ), ( {{0, 0, 0, -1}, {0, 0, -1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}} )}

X = #1 . Τ★[x, 4] &/@mats

{{-x_2, x_1, -x_4, x_3}, {x_3, -x_4, -x_1, x_2}, {-x_4, -x_3, x_2, x_1}}

ΜCom[X[[2]], X[[3]]]/2

ΜCom[X[[3]], X[[1]]]/2

ΜCom[X[[1]], X[[2]]]/2

{-x_2, x_1, -x_4, x_3}

{x_3, -x_4, -x_1, x_2}

{-x_4, -x_3, x_2, x_1}

Mmh. Guess what this does...

ShowMat[Close[mats]]

MF[Com[({{0, -1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, -1}, {0, 0, 1, 0}}), ({{0, 0, 1, 0}, {0, 0, 0, -1}, {-1, 0, 0, 0}, {0, 1, 0, 0}})]/2]

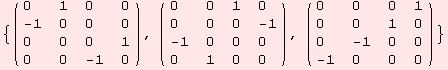
{( {{0, 1, 0, 0}, {-1, 0, 0, 0}, {0, 0, 0, 1}, {0, 0, -1, 0}} ), ( {{0, 0, 1, 0}, {0, 0, 0, -1}, {-1, 0, 0, 0}, {0, 1, 0, 0}} ), ( {{0, 0, 0, 1}, {0, 0, 1, 0}, {0, -1, 0, 0}, {-1, 0, 0, 0}} )}

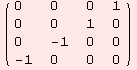
( {{0, 0, 0, 1}, {0, 0, 1, 0}, {0, -1, 0, 0}, {-1, 0, 0, 0}} )

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!