Metric
We treat several metrics simultaneously. A metric is represented by a symmetric matrix, which entries depend on coordinates. Coordinates are denoted ![]() ,
,![]() ,.... The first metric we want to consider is induced by the standard Euclidean scalar product of
,.... The first metric we want to consider is induced by the standard Euclidean scalar product of ![]() . Our manifold is
. Our manifold is ![]() with radius r, which we parametrize in polar coordinates below.
with radius r, which we parametrize in polar coordinates below.
![]()
![]()
![]()
![]()
![( {{r^2 Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, r^2 Cos[x_3]^2, 0}, {0, 0, r^2}} )](../HTMLFiles/index_59.gif)
![]()
Parametrizing ![]() differently, leads to another matrix g. However, the metric are equivalent.
differently, leads to another matrix g. However, the metric are equivalent.
![]()
![]()
![]()
![]()
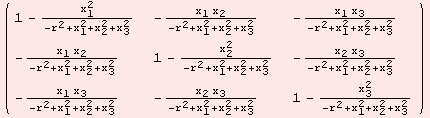
![]()
The computations carried out, are simply the matrix products ![]() .
.![]() .df. In the settings above, df is a 4×3 matrix and
.df. In the settings above, df is a 4×3 matrix and ![]() =
=![]() . For instance
. For instance
![]()
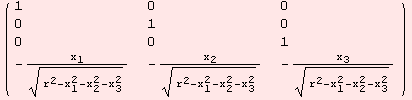
Metrics induced by the embedding of the Riemannian manifold ![]() are intuitive. Another example is the metric of the geometric torus. Below, we define the domain of the parametrization, and the parametrization itself.
are intuitive. Another example is the metric of the geometric torus. Below, we define the domain of the parametrization, and the parametrization itself.
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_78.gif]](../HTMLFiles/index_78.gif)
Next, we present three ways to obtain the metric tensor over the particular domain.
![]()
![]()
![( {{-(R + r Cos[x_2]) Sin[x_1], -r Cos[x_1] Sin[x_2]}, {Cos[x_1] (R + r Cos[x_2]), -r Sin[x_1] Sin[x_2]}, {0, r Cos[x_2]}} )](../HTMLFiles/index_81.gif)
![]()
Along the metric, we have notions such as the angle between two vectors, and the lengths of vectors, or curves. In general, having defined a volume form on the manifold, we can perform integration on subsets of the manifold. But first, lets continue with metrics of index ≥1. The pseudo sphere ![]() of radius r is defined as the points in
of radius r is defined as the points in ![]() which annihilate
which annihilate
![]()
![]()
![]()
![]()
![]()
We plot a part of the manifold for radius r=2.
![]()
![]()
![[Graphics:../HTMLFiles/index_92.gif]](../HTMLFiles/index_92.gif)
![]()
Hyperbolic metric
![]()
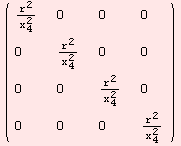
The following space (M,g) is geodesically complete. However, between two points there might not be a connecting geodesic.
![]()
![]()
| Created by Mathematica (December 22, 2006) |