Direct and semi-direct sum

The direct sum of the following two algebras with basis (e_1,e_2) and (f_1,f_2,f_3)  

ShowAd[ad★[a, 2]]

ShowAd[ad★[b, 3]]

( {{0, e_1 a_ (1, 2, 1) + e_2 a_ (2, 2, 1)}, {-e_1 a_ (1, 2, 1) - e_2 a_ (2, 2, 1), 0}} )

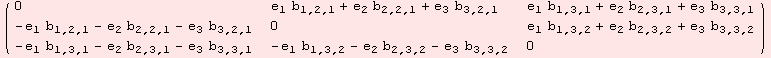
... is the algebra with basis (e_1,e_2,f_1,f_2,f_3) and commutator [e_i,f_j]=0.

ShowAd[ad★[a, 2] ⊕ad★[b, 3]]

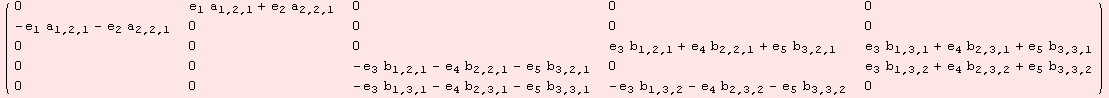
The next example shows the sum of 3-dimensional 1-Heisenberg algebra and (^1,+).

ShowAd[adℋℯ[1]]

ShowAd[adℋℯ[1] ⊕ {{{0}}}]

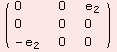
( {{0, 0, e_2}, {0, 0, 0}, {-e_2, 0, 0}} )

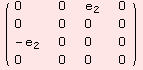
( {{0, 0, e_2, 0}, {0, 0, 0, 0}, {-e_2, 0, 0, 0}, {0, 0, 0, 0}} )

Note, {{{0}}} is the ad tensor of (^1,+).

{{{0}}} . {x} . {y}

{0}

The function we would like to explain is ad∠gl, which establishes the commutator tensor of a semi-direct sum algebra. The procedure makes a subalgebra of _nR act on a n-dimensional ad tensor as a set of derivations.

ShowMat[2 = {({{λ, 0}, {0, -λ}}), ({{0, μ}, {0, 0}}), ({{0, 0}, {υ, 0}})}]

ad = ad∠[0 ad★[a, 2], 2] ;

ShowAd[ad, {x_1, x_2, h, p, q}]

{( {{λ, 0}, {0, -λ}} ), ( {{0, μ}, {0, 0}} ), ( {{0, 0}, {υ, 0}} )}

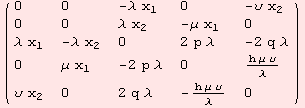
Another example: We setup a general matrix, to act on 1-Heisenberg.

A = Τ★[a, {3, 3}] ; A//MF

ShowAd[ad = ad∠[adℋℯ[1], {A}]]

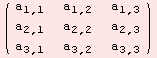
( {{a_ (1, 1), a_ (1, 2), a_ (1, 3)}, {a_ (2, 1), a_ (2, 2), a_ (2, 3)}, {a_ (3, 1), a_ (3, 2), a_ (3, 3)}} )

not jacobian.

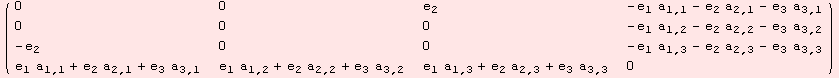
We are interested in the set of possible derivations, thus we demand ad to satisfy the Jacobi identity. It turns out, that the space of derivations is a 6-dimensional vector space with coefficients {a_ (1, 3),a_ (2, 1),a_ (2, 2),a_ (2, 3),a_ (3, 1),a_ (3, 3)}.

ShowAd[ad = LSolve[adJacobi[ad], ad]]

MF[B = ad[[Range[3], Range[3], 4]]]

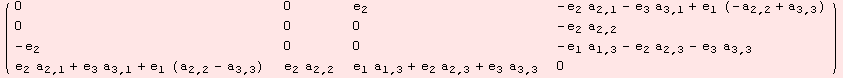
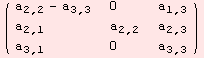
( {{a_ (2, 2) - a_ (3, 3), 0, a_ (1, 3)}, {a_ (2, 1), a_ (2, 2), a_ (2, 3)}, {a_ (3, 1), 0, a_ (3, 3)}} )

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!