Commutator tensor of a matrix algebra

For matrices X,Y the commutator is defined as [X,Y]=X.Y-Y.X. The command glCom abbreviates this easy computation.

{Com[X = ({{1, 0}, {0, -1}}), Y = ({{0, 1}, {0, 0}})], X . Y - Y . X}//ShowMat

{( {{0, 2}, {0, 0}} ), ( {{0, 2}, {0, 0}} )}

Consinder a set of matrices that span a matrix algebra. The function gl2ad yields the corresponding ad tensor of the Lie algebra with respect to the same basis.

2 = {1/2 ({{1, 0}, {0, -1}}), 1/2^(1/2) ({{0, 1}, {0, 0}}), 1/2^(1/2) ({{0, 0}, {1, 0}})} ;

ShowMat[2]

ShowAd[2ad[2]]

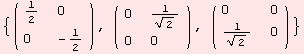
{( {{1/2, 0}, {0, -1/2}} ), ( {{0, 1/2^(1/2)}, {0, 0}} ), ( {{0, 0}, {1/2^(1/2), 0}} )}

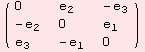
( {{0, e_2, -e_3}, {-e_2, 0, e_1}, {e_3, -e_1, 0}} )

In a previous section, we have used the extremely useful command glAlgebra. Here, we ask the computer to provide a basis for the algebra of upper triangular matrices with trace 0.

ShowMat[mats = Algebra[3, {inv, Tr[#1] &}]]

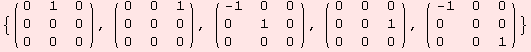
The number of matrices is the dimension of the algebra. Using gl2ad we yield the commutator tensor ad.

ShowAd[ad = 2ad[mats]]

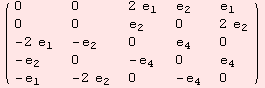
( {{0, 0, 2 e_1, e_2, e_1}, {0, 0, e_2, 0, 2 e_2}, {-2 e_1, -e_2, 0, e_4, 0}, {-e_2, 0, -e_4, 0, e_4}, {-e_1, -2 e_2, 0, -e_4, 0}} )

For instance, the result

ad . {1, 0, 0, 0, 0} . {0, 0, 1, 0, 0}

{2, 0, 0, 0, 0}

coincides with

{Com[mats[[1]], mats[[3]]], (* or *)Com[( {{0, 1, 0}, {0, 0, 0}, {0, 0, 0}} ), ( {{-1, 0, 0}, {0, 1, 0}, {0, 0, 0}} )]}//ShowMat

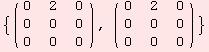
{( {{0, 2, 0}, {0, 0, 0}, {0, 0, 0}} ), ( {{0, 2, 0}, {0, 0, 0}, {0, 0, 0}} )}

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!