Moments Defined by Subdivision Curves

Figure: We compute the exact area, centroid, and inertia of the 2-dimensional sets bounded by subdivision curves. The illustration shows the principle axes of the inertia tensor drawn at the centroid of the area; five different subdivision schemes are used to demonstrate the universality of our derivation.

Abstract: We derive the (d+2)-linear forms that compute the moment of degree d of the area enclosed by a subdivision curve in the plane. We circumvent the need to solve integrals involving the basis function by exploiting a recursive relation and calibration that establishes the coefficients of the form within the nullspace of a matrix.

For demonstration, we apply the technique to the dual three-point scheme, the interpolatory C¹ four-point scheme, and the dual C² four-point scheme.

Moments Defined by Subdivision Curves *	moments_def...pdf	670 kB
Moments Defined by Subdivision Curves (on viXra.org)	viXra:1407.0163	link
Moments Defined by Example Subdivision Curves	viXra:1407.0027	link
Subdivision and Moments Implementation (Mathematica 9)	moments_curves.zip	55 kB

* latest version, modified last on July 28th, 2014

The first author was partially supported by personal savings accumulated during his visit to the Nanyang Technological University as a visiting research scientist in 2012–2013. He'd like to thank everyone who worked to make this opportunity available to him.

Beauty is the first test;
There is no permanent place
for ugly mathematics.
Godfrey Harold Hardy

The moments derived in the article have diverse applications:

• The formulas allow to design subdivision curves with exact area, centroid, and inertia.
• By translation of control points, curves can be deformed subject to preservation of moments.
• The set bounded by a subdivision curve extruded along the interval [a,b] of the z-axis has known moment.
• Countless computer games use planar graphics and physics. If a subdivision curve is the contour of an animated entity, our formulas help to make the motion more plausible. However, our formula assumes constant mass density across the interior.

Our article is structured as follows. First, we recap the basics of curve subdivision: the basis function of a scheme, and refinement matrices. Chaikin's scheme serves as an example. Then, we derive the formula for the moment of degree d for binary, stationary subdivision schemes. We demonstrate the practicability of our formalism on several popular schemes. The computation of moment values defined by a number of simple example curves serves as a reference for alternative implementations.

The schemes that are covered by our treatment are listed here:

Scheme for curves	Subdivision weights	Remark
linear B-spline		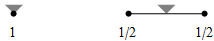interpolatory, results in a polygon
quadratic B-spline Chaikin 1965		dual
cubic B-spline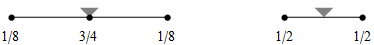
Three-point scheme Hormann/Sabin 2008, and Quartic B-spline		dual, ω=1/32, ω=-1/48, quadratic precision
C1 four-point scheme Dubuc 1986, Dyn/Gregory/Levin 1987		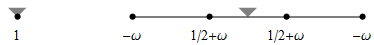interpolatory, default ω=1/16, smooth for 0<ω<0.192729...
C2 four-point scheme Dyn/Floater/Hormann 2005		dual, default ω=1/128, smooth at least for 0<ω<1/48
C2 six-point scheme Weissman 1990		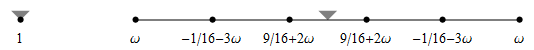interpolatory, default ω=3/256, and ω=1/96

The more you collaborate,
the more competitive you become.
Simon Anholt

Figure: The monomials 1, x, y, x², xy, y² integrated over the domain bounded by subdivision curves give the moments.

Future work

Our article does not feature subdivision schemes with non-homogeneous rules. Two examples immediately come to mind:

• Cubic B-spline subdivision is sometimes used with crease vertices: The scheme is interpolatory at the crease vertex (instead of applying the [1 6 1]/8 averaging mask). For a facet adjacent to a crease vertex, different multilinear forms need to be derived in order to determine the contribution of the facet to the global moment.
• In his paper Polynomial generation and Quasi-interpolation in stationary non-uniform subdivision, Adi Levin blends the C1 four-point scheme by Dubuc with the cubic B-spline scheme. In order to compute the moments of the set enclosed by the curve, four special forms have to be derived.

Remark: Our subsequent preprint covers the area forms for the schemes that are listed here as future work.

We believe that the best product decisions are made
by the people who are actually doing the work.
Valve