Biinvariant Distance Vectors

Abstract: We construct biinvariant vector valued functions of relative distances using the influence matrix, and the Mahalanobis distance defined by scattered sets of points on Lie groups. The functions are invariant under all group operations. Distance vectors define an ordering of the points in the scattered set with respect to a group element. Applications are classification, inverse distance weighting, and the construction of generalized barycentric coordinates for the purpose of deformation, and domain transfer.

a)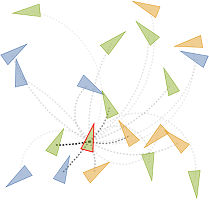

b)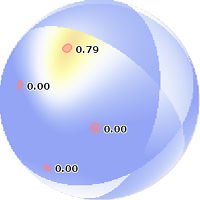

c)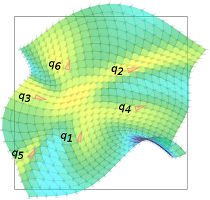

Figure: Applications of biinvariant distance vectors and weightings: a) classification task in the Lie group SE(2), b) kriging function f:RP²->R on the real projective space based on four control points with associated values, c) smooth domain transfer [0,1]² subset R² to SE(2) covering based on control points of the form p_i=(px_i, py_i) in R² mapped to q_i=(px_i, py_i, theta_i) in SE(2) covering for i=1,...,6.

Biinvariant Distance Vectors *	biinvariant_dis...pdf	2.3 MB
	viXra:2007.0043	link
	video on youtube	link

* The author thanks Kai Hormann for his valuable feedback that led to significant improvements in the article, and for the kind invitation to join the CSF workshop.

What can be conceived
can be created.
from a 1980 car ad

The article discusses four types of distance vectors:

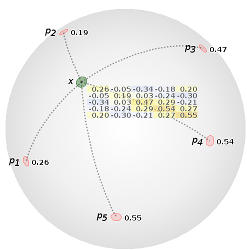
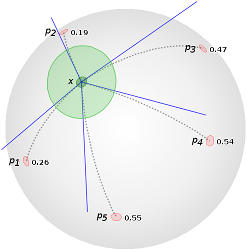
The leverages are the diagonal elements of the influence matrix at point x. The values are constrained to the unit interval [0, 1].	The Mahalanobis distance is the evaluation of the tangent vectors log_x(p_i) subject to the positive definite bilinear form at x.
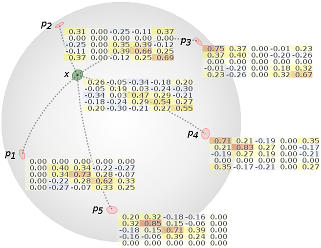
An element of the Harbor distance vector is the Frobenius norm of the difference between the influence matrix at x and the influence matrix at the respective landmark point.	The Garden distance vector contains the evaluation of the Mahalanobis distance at the landmark points and the tangent vector in the tangent space at p_i that points to x.

The impossible often has a kind of integrity to it
which the merely improbable lacks.
Douglas Adams

     

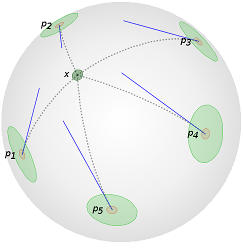
Figure: The points in P from SE(2) are color coded according to their position in the ordering based on their relative distance from x in SE(2). From left to right: Leverage distances, Harbor distances, Garden distances

What you read when you don't have to
determines what you will be
when you can't help it.
Oscar Wilde

The author was partially supported by personal savings accumulated during his employment at ETH Zürich in 2017–2019. He'd like to thank everyone who worked to make this opportunity available to him.