Biinvariant Generalized Barycentric Coordinates on Lie Groups

Inverse Distance Weighting [1968 Shepard]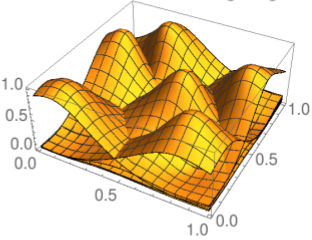

Inverse Distance Coordinates viXra:2002.0929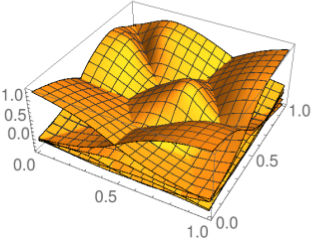

Biinvariant Coordinates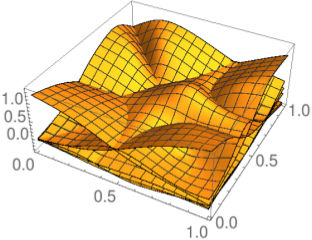

Figure: Basis functions of inverse distance weighting, inverse distance coordinates, and biinvariant coordinates with exponent 2 for an example set of six points in the unit square.

Abstract: We construct biinvariant generalized barycentric coordinates for scattered sets of points in any Lie group. The coordinates are invariant under left-action, right-action, and inversion, and satisfy the Lagrange property. The construction does not utilize a metric on the Lie group, unlike inverse distance coordinates. Instead, proximity is determined in a vector space of higher dimensions than the group using the Euclidean norm. The coordinates that we propose are an inverse to the unique, biinvariant weighted average in the Lie group.

Biinvariant Generalized Barycentric Coordinates on Lie Groups	biinvariant_gen...pdf	2.5 MB
	viXra:2002.0584	link
	youtube	link

Graders received some elegant solutions,
some not-so-elegant solutions,
and some so not elegant solutions.
Delong Meng

There is light at the end of the tunnel,
but it is moving away at speed c.

The author was partially supported by personal savings accumulated during his employment at ETH Zürich in 2017–2019. He'd like to thank everyone who worked to make this opportunity available to him.